Multiple Choice
Identify the choice that best completes the statement or answers
the question.
|
|
|
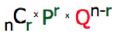 Using the formula above, answer the
questions that follow.
|
|
|
1.
|
The number of trials is
a. | n | b. | C | c. | r | d. | P | e. | Q | f. | n-r | g. | Not listed on its
own |
|
|
|
2.
|
The number of failures is
a. | n | b. | C | c. | r | d. | P | e. | Q | f. | n-r | g. | Not listed on its
own |
|
|
|
3.
|
The probability of success is
a. | n | b. | C | c. | r | d. | P | e. | Q | f. | n-r | g. | Not listed on its
own |
|
|
|
4.
|
The number of successes is
a. | n | b. | C | c. | r | d. | P | e. | Q | f. | n-r | g. | Not listed on its
own |
|
|
|
5.
|
The number of ways “n” trials can yield “r” number of
successes is
a. | n | b. | C | c. | r | d. | P | e. | Q | f. | n-r | g. | Not listed on its
own |
|
|
|
6.
|
This formula is used to calculate a specific probability for which
probability distribution?
a. | Uniform | b. | Binonmial | c. | Geometric | d. | Hypergeometric | e. | Normal
(symetrical) |
|
|
|
7.
|
The expected number of successes for the formula above is:
a. | Q ÷ P | b. | X • P(x) | c. | r •
(n/a) | d. | n • P | e. | Indeterminable |
|
|
|
8.
|
Which of the following statements is false?
a. | Geometric trials contiue until there is a success, then stop. | b. | In binomial
probability distributions, trials can be categorized as a success or a failure. | c. | The probability of
success is constant for all distributions | d. | Essentially, the calculation of the expected
number of successes is the same for hypergeometric and binomial
distributions. |
|
|
|
9.
|
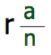 The formula above is expected value for a
hypergeometric distribution. The probability of success is
|
|
|
10.
|
Why does the binomial formula contain the combination formula
nCr or trialsCsuccesses?
a. | To count the number of successes in “n” number of
trials | b. | To calculate the probability of success | c. | To count of the
number of different ways a series of trials could produced the desired number of
successes | d. | To count the number of orders in which the success can occur in a set of
trials. |
|
|
|
11.
|
The number of trials required for to calculate P(x) must be known outset for which of the following
distributions?
a. | Binomical | b. | Geometric | c. | Hypergeometric | d. | All of these | e. | None of
these |
|
|
|
12.
|
Of all the probability formulas, which one is cumulative and returns a value
that measures the probability of “r” number of successes or less?
a. | The binomial probability formula | b. | The geometric probability
formula | c. | The hypergeometric probability formula | d. | All of the above | e. | None of the
above |
|
|
|
13.
|
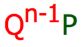 For the formula above, why is Q raised to
the power of n-1 a. | This is the number of failures for a geometric probability
distribution | b. | This is one less trial than the total “n”, to account for the final trial
that must be a success | c. | All the above are correct | d. | All of the above are
false |
|
|
|
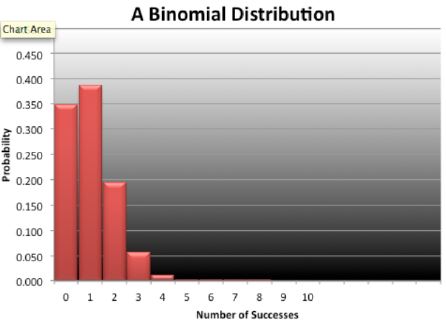 Use the graph above to answer the
following questions.
|
|
|
14.
|
Based on the graph of the binomial distribution, how many trials were
there?
a. | 10 | b. | 8 | c. | 4 | d. | It’s impossible to
estimate |
|
|
|
15.
|
Based on the graph of the binomial distribution, what was the probability of
success?
|
|
|
16.
|
What is the probability of achieving two or more successes in ten
trials?
a. | ~19% | b. | ~28% | c. | ~72% | d. | None of these is
correct |
|
|
|
17.
|
To calculate the precise value of the probability of achieving two or more
successes in ten trials (as shown in this graph), you would use
10C2(0.10)2(0.90)8.
a. | True | b. | False | c. | Can’t be
determined |
|
|
|
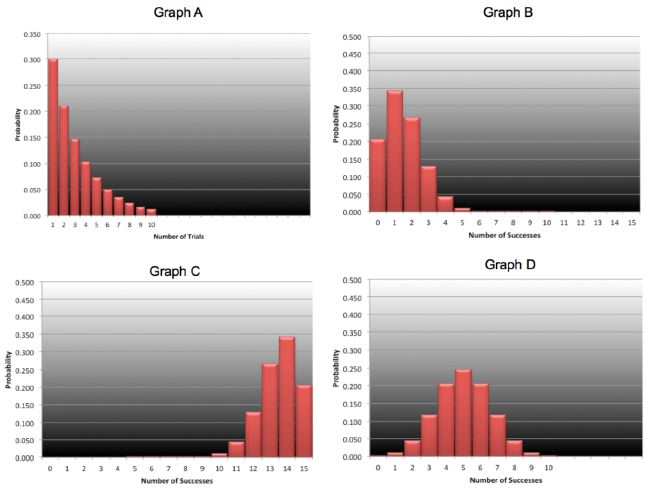
Use the graphs below to answer the following questions. Click the image
to pop out the image.
|
|
|
18.
|
Which graph is for a geometric probability distribution?
a. | Graph A | b. | Graph B | c. | Graph
C | d. | Graph D |
|
|
|
19.
|
For which distribution is the probability of success 50%?
a. | Graph A | b. | Graph B | c. | Graph
C | d. | Graph D |
|
|
|
20.
|
Which two graphs have P and (1-P) respectively, as their probabilities of
success? In other words, which graph has P as the probability of success, and which other graph has
the complement of P as its probability of success?
a. | A and B | b. | A and C | c. | A and
D | d. | B and C | e. | B and D | f. | D and
C |
|
|
|
21.
|
Which graph is for a binomial probability distribution?
a. | Graph A | b. | Graph B | c. | Graph A and
B | d. | Graph B and C | e. | All of them | f. | All but graph
A |
|
|
|
22.
|
What is the probability of success for the geometric probability
distribution?
a. | 30% | b. | 70% | c. | 50% | d. | 15% | e. | Can’t be
determined |
|
Multiple Response
Identify one or more choices that best complete the statement or
answer the question.
|
|
|
Use the formulas below to answer the questions that
follow. Click the image to pop out the formulas for
easier viewing.

|
|
|
23.
|
Which of the formula(s) above would you use to solve the following
problem:
A casino has created the following game
involing two dice. The rolls and payouts are listed. What is the most you would pay to play this
game?
Die
Roll | Payout | 2 or 12 | $20 | 6 | $5 | 7 | $4 | 8 | $5 | doubles | $10 | All else | $0 | | |
|
|
|
24.
|
Which of the formula(s) above would you use to solve the following
problem:
A casino has created the following game
involing two dice. How many times would you expect to win this game if you played ten
times?
Die Roll | Payout | 2 or 12 | $20 | 6 | $5 | 7 | $4 | 8 | $5 | doubles | $10 | All else | $0 | | |
|
|
|
25.
|
Which of the formula(s) above would you use to solve the following
problem:
If your crush tells you that 95% of everybody
you ask out will reject you (your crush isn’t very nice), how many people are you going to have
to ask out to get a date to the prom?
|
|
|
26.
|
Which of the formula(s) above would you use to solve the following
problem:
If you have a 50% chance of passing an exam in
a course you’ve never attended, and a university degree has 40 half-year courses, what are the
chances of you earning your degree without ever spending a day in school? (Assume passing the exam
earns you the credit).
|
|
|
27.
|
Which of the formula(s) above would you use to solve the following
problem:
If you have a 50% chance of passing an exam in
a course you’ve never attended, and a university degree has 40 half-year courses, how many
final exams would you expect to pass without ever spending a day in school?
|
|
|
28.
|
Which of the formula(s) above would you use to solve the following
problem:
The engineering and quality control department
of a manufacturing firm is testing for defects. The particular product is a package containing an assortment of fasteners that customers can buy. They contain three different types of screws and
bolts (10 small, 20 medium, and 5 large). If past performance indicates a defect rate of 1%, 0.4%, and
0.5% per fastener, respectively, what should this particular product sample's acceptable defect rate
be?
|
|
|
29.
|
Which of the formula(s) above would you use to solve the following
problem:
The engineering and quality control department
of a manufacturing firm is testing for defects. The particular product is a package containing an
equal assortment of fasteners that customers can buy. They contain three different types of screws and
bolts (10 small, 20 medium, and5 large). Past performance indicates a defect rate of 1%, 0.4%, and
0.5% per fastener, respectively. If a bin containing all the fasteners prior packaging is tested, and it contains
100 small fasteners, 150 medium ones, and 75 large ones,
a) What is the probability in a
sample of 9 fasteners, that you will have exactly 3 of each kind?
b) How many of each kind
would you expect?
c) What should the defect rate be in the sample that is most likely to be
drawn?
|
|
|
30.
|
Which of the formula(s) above would you use to solve the following
problem:
The engineering and quality control department
of a manufacturing firm is testing for defects. The particular product is a package containing an assortment of fasteners that customers can buy. They contain three different types of screws and
bolts (10 small, 20 medium, and 5 large). Past performance indicates a defect rate of 1%, 0.4%, and
0.5% per fastener, respectively. If a giant bin containing all the fasteners prior packaging is tested, and it
contains 10,000 small fasteners, 15,000 medium ones, and 7,500 large ones,
a) If you tested
100 small fasterns one at a time, what are the chances you’d never find a defect until the very
end?
b) How many should you find in 100 samples?
|
|
|
31.
|
Which of the formula(s) above would you use to solve the following
problem:
You are conducting a marketing survey for a
family sedan. To avoid statistical discrepancy and sampling bias, you need to randomly sample 1,001
people who drive Toyotas and are a parent in a family of four (two adults and two children), which is
only 4.7% of the total population. If in your experience you know that only 20% of people comply with
a telephone survey request, how many people do you need to call to complete this task?
|