Name: 
 

Intro to Probability


Multiple Choice
Identify the choice that best completes the statement or answers the question.
 
 
The following is information gathered from a survey for Boult’s Pizza Pizzaz. Answer the questions that follow.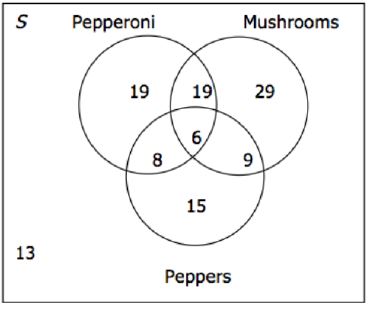

nar001-1.jpg
 

 1. 
How many customers were surveyed?
a.
105
b.
118
c.
99
d.
112
 

 2. 
How many people surveyed like pepperoni and mushrooms?
a.
19
b.
48
c.
25
d.
65
e.
90
 

 3. 
How many people surveyed prefer pepperoni or peppers?
a.
34
b.
32
c.
62
d.
76
e.
42
 

 4. 
How many people surveyed prefer either mushrooms or peppers?
a.
44
b.
86
c.
53
d.
71
 

 5. 
How many people surveyed do not like all three toppings?
a.
13
b.
19
c.
99
d.
112
 

 6. 
How many people surveyed like pepperoni?
a.
19
b.
46
c.
52
d.
13
 

 7. 
How many people enjoy either pepperoni or peppers but not mushrooms?
a.
42
b.
62
c.
34
d.
76
 

 8. 
Given that a survey respondent likes pepperoni, what is the probability that he or she likes mushrooms?
a.
19/105
b.
25/105
c.
25/118
d.
63/52
e.
63/90
f.
25/52
 

 9. 
Given that a survey respondent likes pepperoni and mushrooms, what is the probability that he or she likes peppers?
a.
23/38
b.
6/15
c.
6/42
d.
6/25
e.
23/90
 

 10. 
Given that a survey respondent likes pepperoni or mushrooms, what is the probability that he or she likes peppers?
a.
23/38
b.
6/15
c.
6/42
d.
6/25
e.
23/90
 

 11. 
The specific outcome which is most likely to occur. This is a definition of
a.
Theoretical probability
b.
Empirical probability
c.
Subjective probability
d.
An outcome
e.
An event
f.
Probability
g.
Expected value
h.
The sample space
 

 12. 
The result of an empirical trial. This is a definition of
a.
Theoretical probability
b.
Empirical probability
c.
Subjective probability
d.
An outcome
e.
An event
f.
Statistical discrepancy.
g.
Expected value
h.
The sample space
 

 13. 
The chance of an event occuring. This is a definition of
a.
Theoretical probability
b.
Empirical probability
c.
Subjective probability
d.
An outcome
e.
An event
f.
Statistical discrepancy
g.
Expected value
h.
The sample space
 

 14. 
A specific outcome sought by a trial or experiement. This is a definition of
a.
Theoretical probability
b.
Empirical probability
c.
Subjective probability
d.
An outcome
e.
An event
f.
Statistical discrepancy
g.
Expected value
h.
The sample space
 

 15. 
Everything that could happen. This is a definition of
a.
Theoretical probability
b.
Empirical probability
c.
Subjective probability
d.
An outcome
e.
An event
f.
Statistical discrepancy
g.
Expected value
h.
The sample space
 

 16. 
If event A is the probability of getting two heads (HH) with two tosses of a coin, then the probability of (A’) must be the probability of getting:
a.
TT
b.
HT
c.
TH
d.
HH
e.
None of these answers is correct
 

 17. 
Which of the following is true about statistical discrepancy?
a.
It is a natural phenomenon that can be eliminated
b.
There is nothing you can do about it
c.
The greater the statistical discrepancy, the higher the accuracy
d.
The greater the number of trials, the greater your discrepancy
e.
It is the difference between observed empirical probability, and theoretical probability.
 

 18. 
Which of the following calculations can never be used to find the probability of either A or B?
a.
P(A) + P(B) - 2P(A ∩ B)
b.
P(A ∪ B) - P(A ∩ B)
c.
P(A) + P(B)
d.
P(A) x P(B)
 

 19. 
Which of the following calculation can always be used to find the probability of A or B?
a.
n(A) + n(B) - n(A n B)
n(S) + n(S)  -   n(S)
b.
P(A ∪ B) - P(A ∩ B)
c.
P(A) + P(B)
d.
P(A) x P(B)
e.
(a) and (b) are correct.
 

 20. 
What should this diagram indicate to you?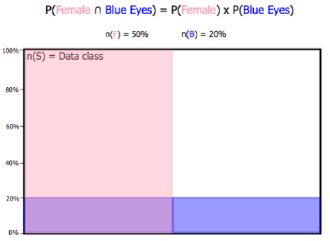

mc020-1.jpg
a.
When the proportion of one characteristic (like blue eyes) is consistent among all groups in the sample space n(S), you can multiply its share of the total sample space with another group’s share of the sample space (like Females) to find out how many members of the second group have blue eyes.
b.
P(A ∩ B) = (P(A) x P(B) must not work all the time.
c.
Why P(A ∩ B) = (P(A) x P(B) works to calculate the probability of independent events occuring simultaneously.
d.
All of the above are correct.
 

 21. 
Take the following list.

P(A ∩ B)     
P(A ∪ B)
P(A | B)     
P(A ∪ B) - P(A ∩ B)     

Which of the following lists of narrative descriptions match correctly to the list above? The probabilities of...
a.
A or B or both
A given B
either A or B exclusively
A and B
d.
A or B or both
A given B
A and B
either A or B exclusively
b.
A or B or both
A and B
A given B
either A or B exclusively
e.
A and B
A or B or both
A given B
either A or B exclusively
c.
A and B
either A or B exclusively
A given B
A or B or both
f.
either A or B exclusively
A and B
A or B or both
A given B
 

 22. 
In a given sample space n(S), with two subsets (event A and event B), which is more likely of occuring:
a.
P(A ∩ B)
b.
P(A ∪ B)
c.
P(A | B)
d.
P(A ∪ B) - P(A ∩ B)
e.
None of these is the correct answer
f.
It depends, either (b) or (c) could be larger, and (b) will always be larger than (d).
 



 
Check Your Work     Start Over